Simulador
0: Rever alguns sólidosOffline (necessita do Geogebra instalado)
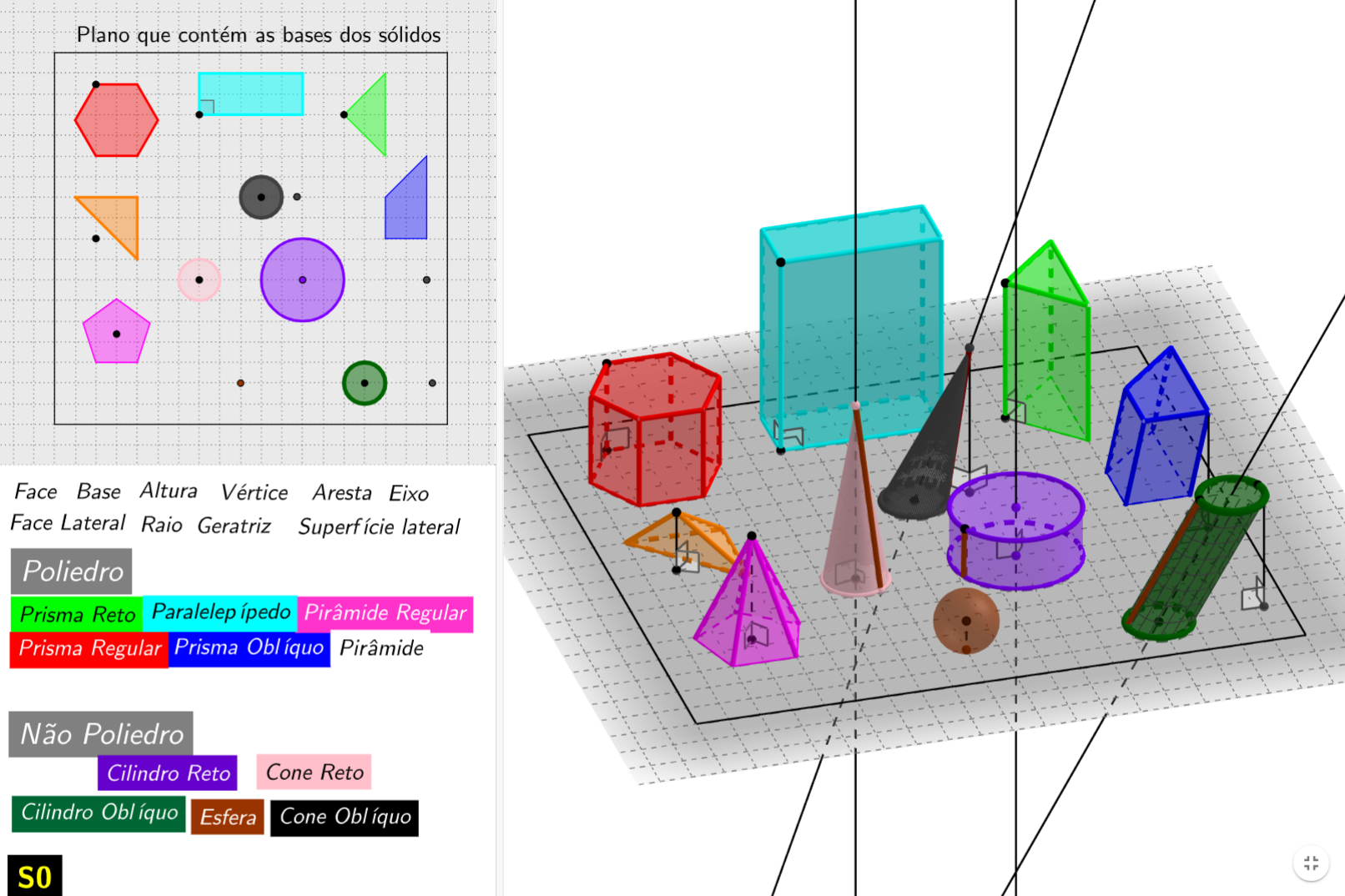
Contém exemplos dos
diversos
sólidos conhecidos, com as designações dos sólidos e dos seus elementos.
A interação é feita com o ponteiro do rato na região 3D:
• Rodar o rato faz zoom in/out;
• Premir o botão direito do rato e mexer o rato faz rodar a vista 3D.
A interação é feita com o ponteiro do rato na região 3D:
• Rodar o rato faz zoom in/out;
• Premir o botão direito do rato e mexer o rato faz rodar a vista 3D.
Atividade 0.1 | Atividade 0.2 | Atividade 0.3
 Simulador 1:
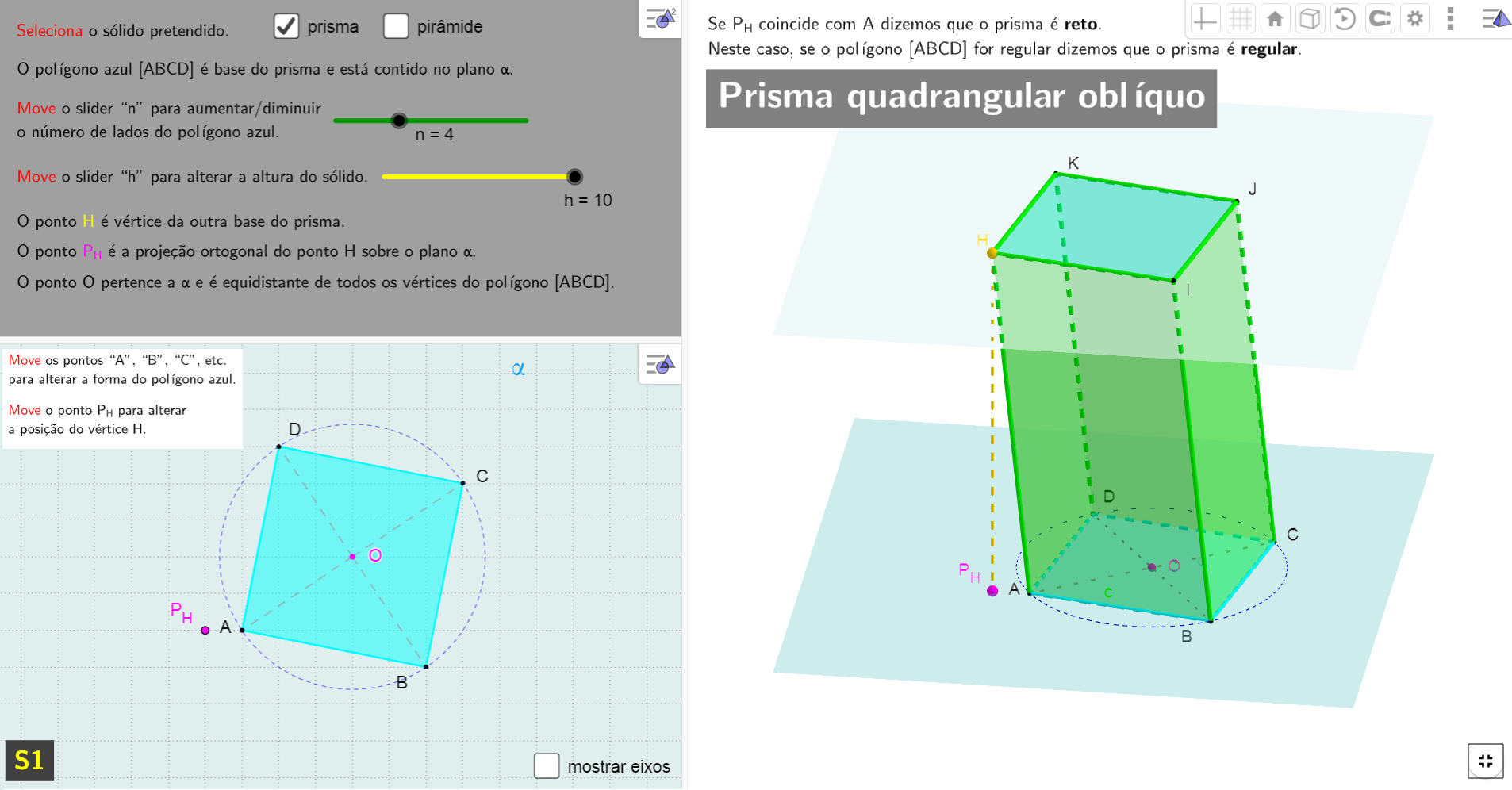
Classificação de Prismas e PirâmidesContém exemplos
de
diversos prismas e pirâmides, com as designações dos sólidos
específicas das suas características.
A interação é feita: Na região 2D: • Selecionar o sólido pretendido; • Deslizar os sliders para alterar as suas medidas/características (nº de lados do polígono da base e altura); • Mover os pontos A, B, C, ... para alterar a forma do polígono da base; • Mover o ponto PH para alterar a posição da projeção do vértice H sobre o plano da base do sólido; Na região 3D: • Rodar o rato faz zoom in/out; • Premir o botão direito do rato e mexer o rato faz rodar a vista 3D. |
Simulador 2: Sólidos
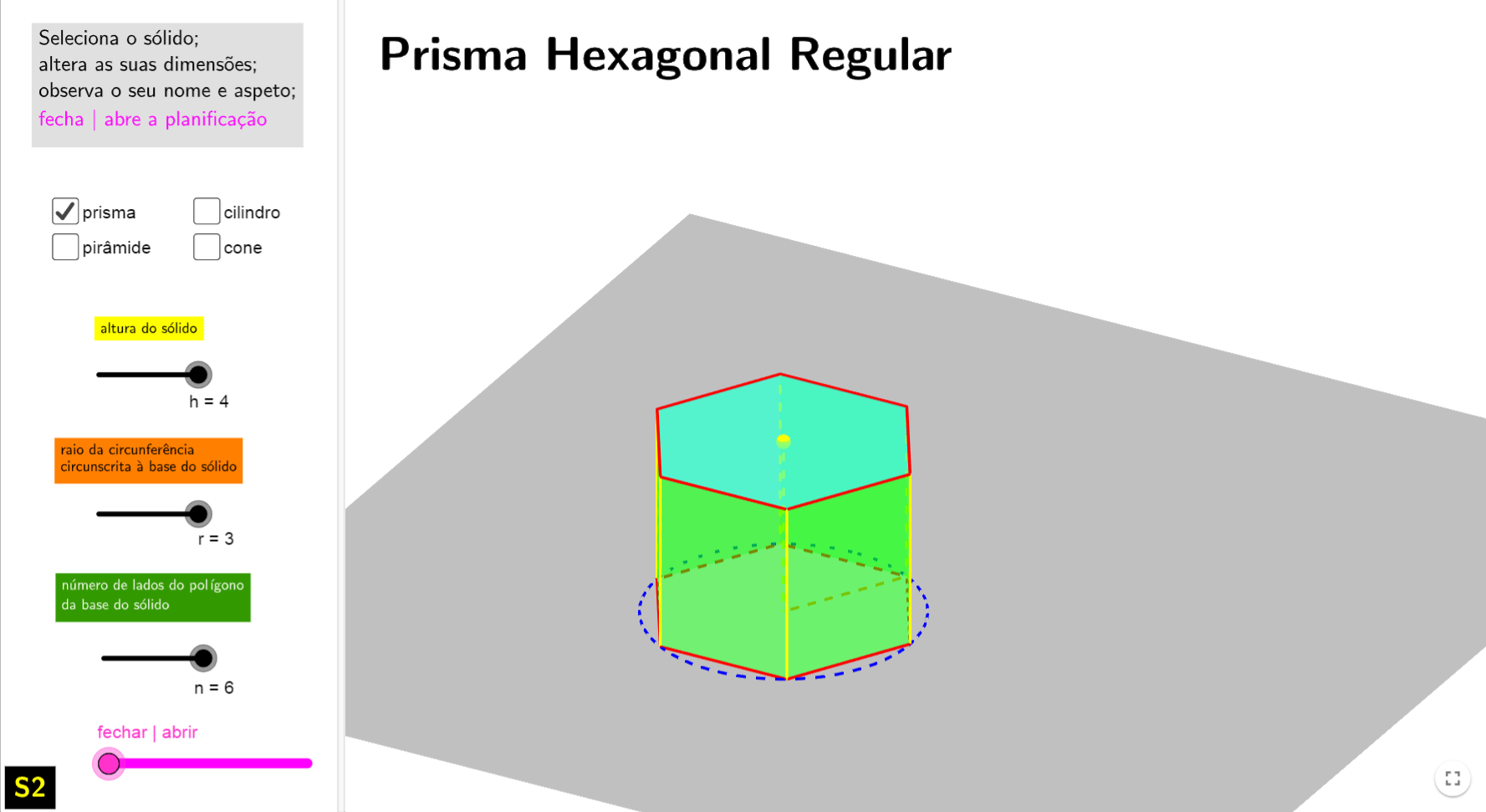
e suas planificaçõesPermite conhecer a
designação e a planificação de alguns sólidos retos/regulares em função
das suas medidas.
A interação é feita:
Na região 2D:
• Selecionar o sólido pretendido;
• Deslizar os sliders para alterar as suas medidas/características;
• Deslizar o slider cor de rosa para fazer “embrulhar/desembrulhar” o sólido com a sua planificação (com o slider todo para a direita a figura no plano cinzento (que contém a base do sólido) é a planificação do sólido;
Na região 3D
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer rato faz rodar a vista 3D.
A interação é feita:
Na região 2D:
• Selecionar o sólido pretendido;
• Deslizar os sliders para alterar as suas medidas/características;
• Deslizar o slider cor de rosa para fazer “embrulhar/desembrulhar” o sólido com a sua planificação (com o slider todo para a direita a figura no plano cinzento (que contém a base do sólido) é a planificação do sólido;
Na região 3D
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer rato faz rodar a vista 3D.
Atividade 2.1 | Atividade 2.2
Simulador
3:
Princípio de
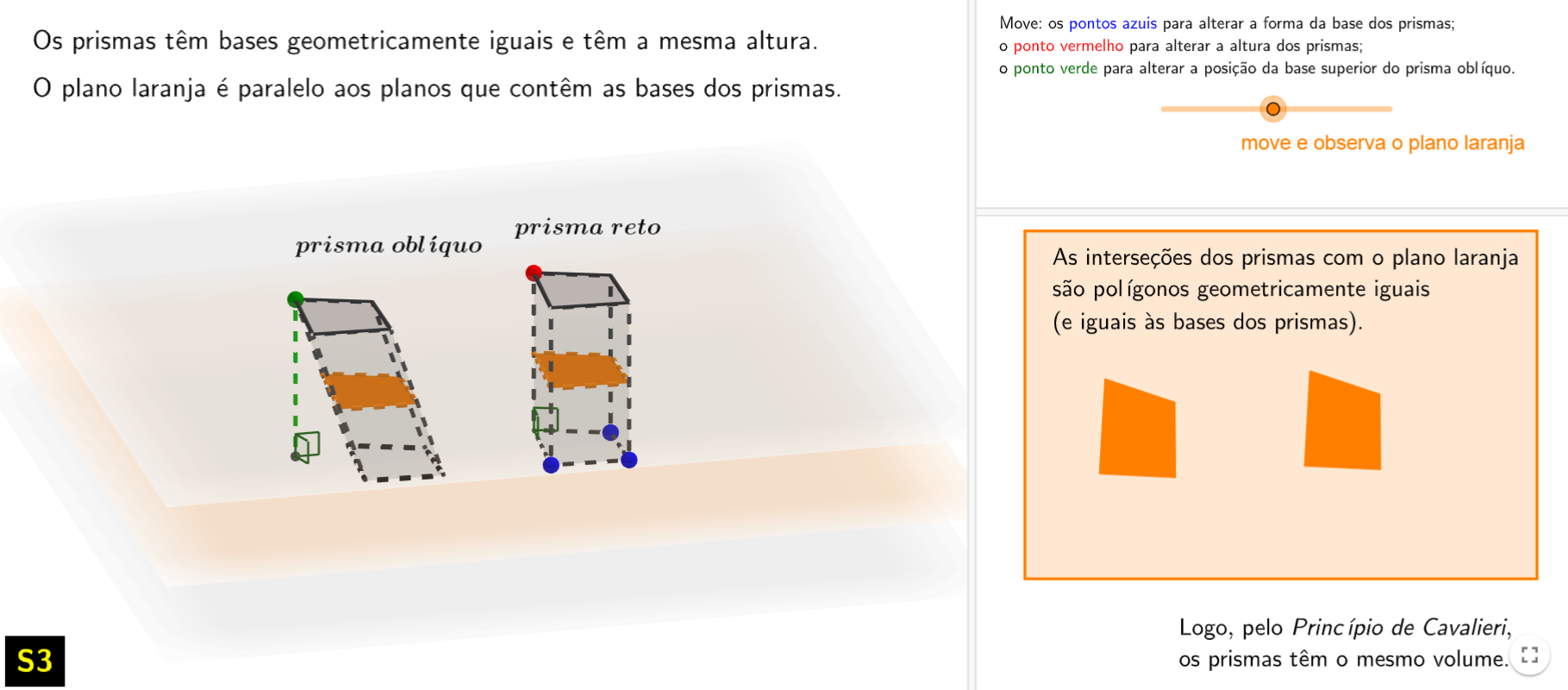
Cavalieri e VolumesIlustra as condições
que
permitem concluir, pelo Princípio de Cavalieri, que dois prismas de
mesma base e mesma altura têm o mesmo volume.
A interação é feita:
Na região 3D com o ponteiro do rato na região 3D:
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer rato faz rodar a vista 3D;
• Mover os pontos azuis permite alterar a forma da base dos prismas;
• Mover o ponto vermelho permite alterar a altura dos prismas;
• Mover o ponto verde permite alterar a posição da base superior do prisma oblíquo (ao sobrepor os ponto verde e vermelho pode tornar-se difícil voltar a mover o ponto verde; neste caso passar o rato sobre os ponto e aguardar que surjam duas setas bidirecionais e perpendiculares);
Na região 2D:
• Deslizar o slider cor de laranja permite alterar a posição do plano de corte cor de laranja, que por sua vez produz as seções apresentadas nas regiões 2D e 3D.
A interação é feita:
Na região 3D com o ponteiro do rato na região 3D:
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer rato faz rodar a vista 3D;
• Mover os pontos azuis permite alterar a forma da base dos prismas;
• Mover o ponto vermelho permite alterar a altura dos prismas;
• Mover o ponto verde permite alterar a posição da base superior do prisma oblíquo (ao sobrepor os ponto verde e vermelho pode tornar-se difícil voltar a mover o ponto verde; neste caso passar o rato sobre os ponto e aguardar que surjam duas setas bidirecionais e perpendiculares);
Na região 2D:
• Deslizar o slider cor de laranja permite alterar a posição do plano de corte cor de laranja, que por sua vez produz as seções apresentadas nas regiões 2D e 3D.
Simulador
4: Volume da
Pirâmide
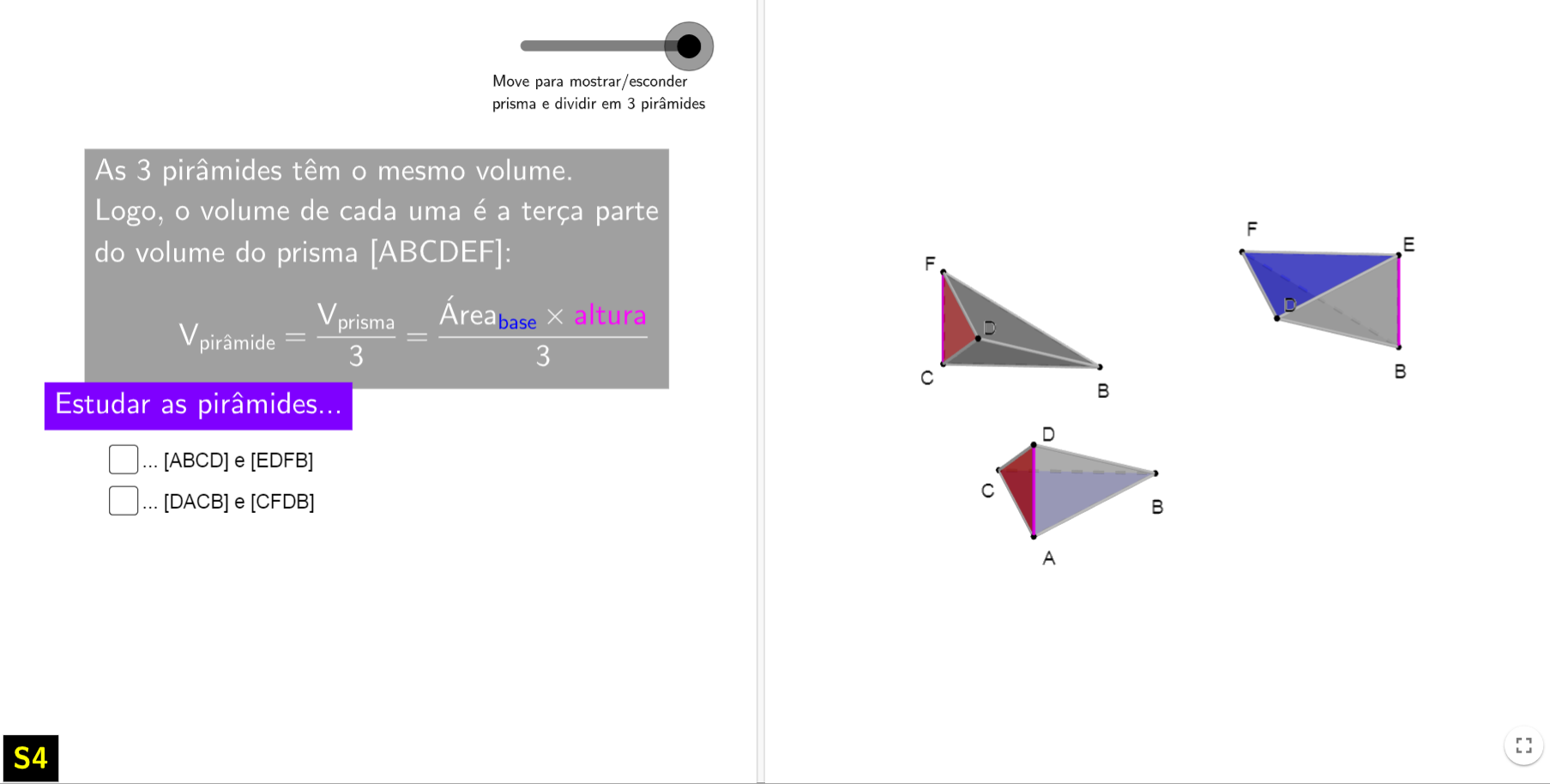
a partir do Prisma Pela divisão de um
prisma
triangular reto em 3 pirâmides triangulares, ilustra as condições que
permitem concluir, pelo Princípio de Cavalieri, que as três têm o mesmo
volume.
A interação é feita:
Na região 3D com o ponteiro do rato na região 3D:
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer rato faz rodar a vista 3D;
• Mover os pontos azuis permite alterar a forma da base do prisma e a sua altura;
Na região 2D:
• Deslizar o slider “move para mostrar/esconder prisma e dividir em 3 pirâmides” separa as 3 pirâmides. Quando o slider se encontra totalmente à direita surgem outras opções:
• Selecionar o par de pirâmides que se pretende mostrar, por ilustração do princípio de Cavalieri, que têm o mesmo volume; após a seleção surge slider roxo:
• Deslizar o slider roxo permite efetuar transformações isométricas a uma das pirâmides, colocando-a numa posição que facilita a apreciação do Princípio de Cavalieri; Quando o slider se encontra totalmente à direita surge slider cor de laranja:
• Deslizar o slider cor de laranja permite alterar a posição do plano de corte cor de laranja; a observação das seções produzidas é feita apenas na região 3D.
A interação é feita:
Na região 3D com o ponteiro do rato na região 3D:
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer rato faz rodar a vista 3D;
• Mover os pontos azuis permite alterar a forma da base do prisma e a sua altura;
Na região 2D:
• Deslizar o slider “move para mostrar/esconder prisma e dividir em 3 pirâmides” separa as 3 pirâmides. Quando o slider se encontra totalmente à direita surgem outras opções:
• Selecionar o par de pirâmides que se pretende mostrar, por ilustração do princípio de Cavalieri, que têm o mesmo volume; após a seleção surge slider roxo:
• Deslizar o slider roxo permite efetuar transformações isométricas a uma das pirâmides, colocando-a numa posição que facilita a apreciação do Princípio de Cavalieri; Quando o slider se encontra totalmente à direita surge slider cor de laranja:
• Deslizar o slider cor de laranja permite alterar a posição do plano de corte cor de laranja; a observação das seções produzidas é feita apenas na região 3D.
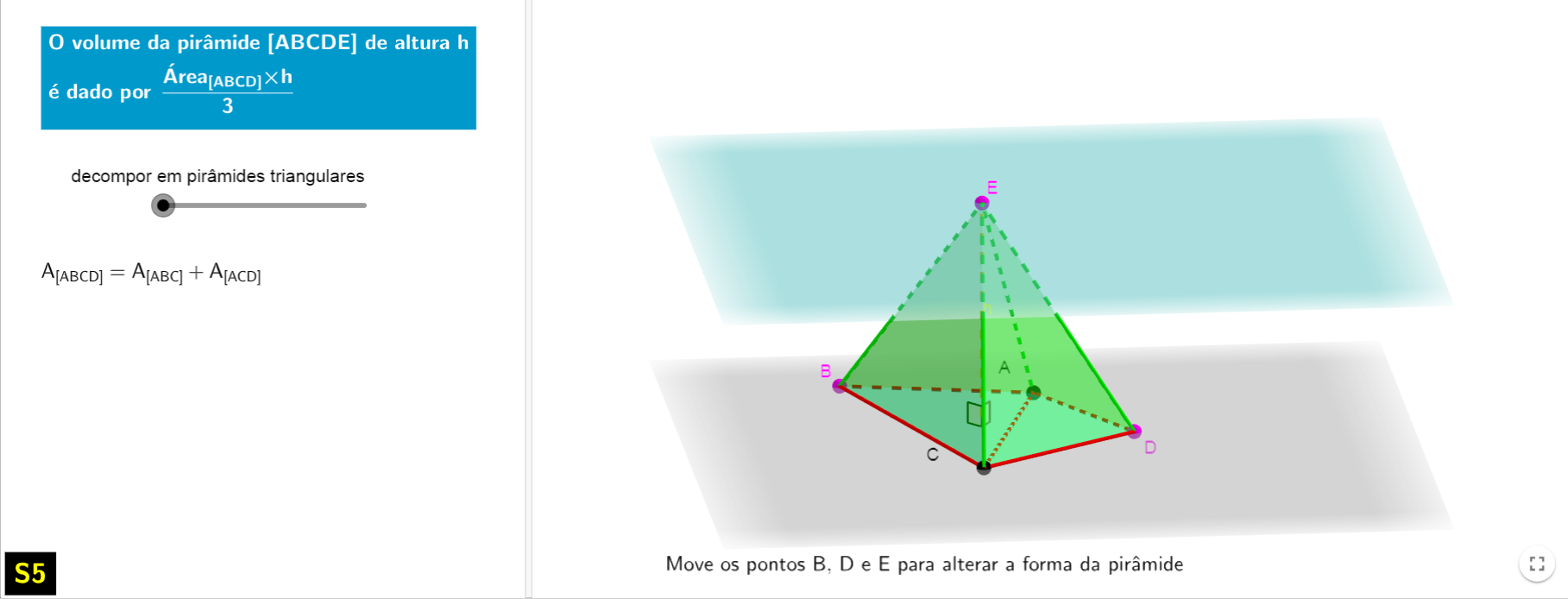
A partir de uma pirâmide cuja base é um quadrilátero e a partir da divisão deste por uma diagonal, ilustra a divisão da pirâmide em duas de bases triangulares e apresenta a demonstração da fórmula do volume da pirâmide.
A interação é feita:
Na região 3D com o ponteiro do rato na região 3D:
• Rodar do rato faz zoom in/out;
• Premir o botão direito do rato e mexer o rato faz rodar a vista 3D;
• Mover os pontos cor de rosa permite alterar a forma da base da pirâmide e a sua altura;
Na região 2D:
• Deslizar o slider “decompor em pirâmides triangulares” separa as 2 pirâmides e apresenta a demonstração.
Contém exemplos de pirâmide e prisma de bases iguais inscritas na mesma circunferência. Apresenta cálculos relativos aos perímetros e áreas do polígono da base desses sólidos, bem como do círculo onde está inscrita a base do sólido.
A interação é feita:
Na região 2D:
• Deslizar o slider "número de lados do polígono da base" faz aumentar/diminuir esse número, entre 3 e 150;
Na região 3D, com o ponteiro do rato na região 3D:
• Premir o botão direito do rato e mexer o rato faz rodar a vista 3D.
Simulador
7: Volumes e Áeas de
Superfícies de Sólidos Retos/Regularesvalores exatos (7A) e valores aproximados (7B)
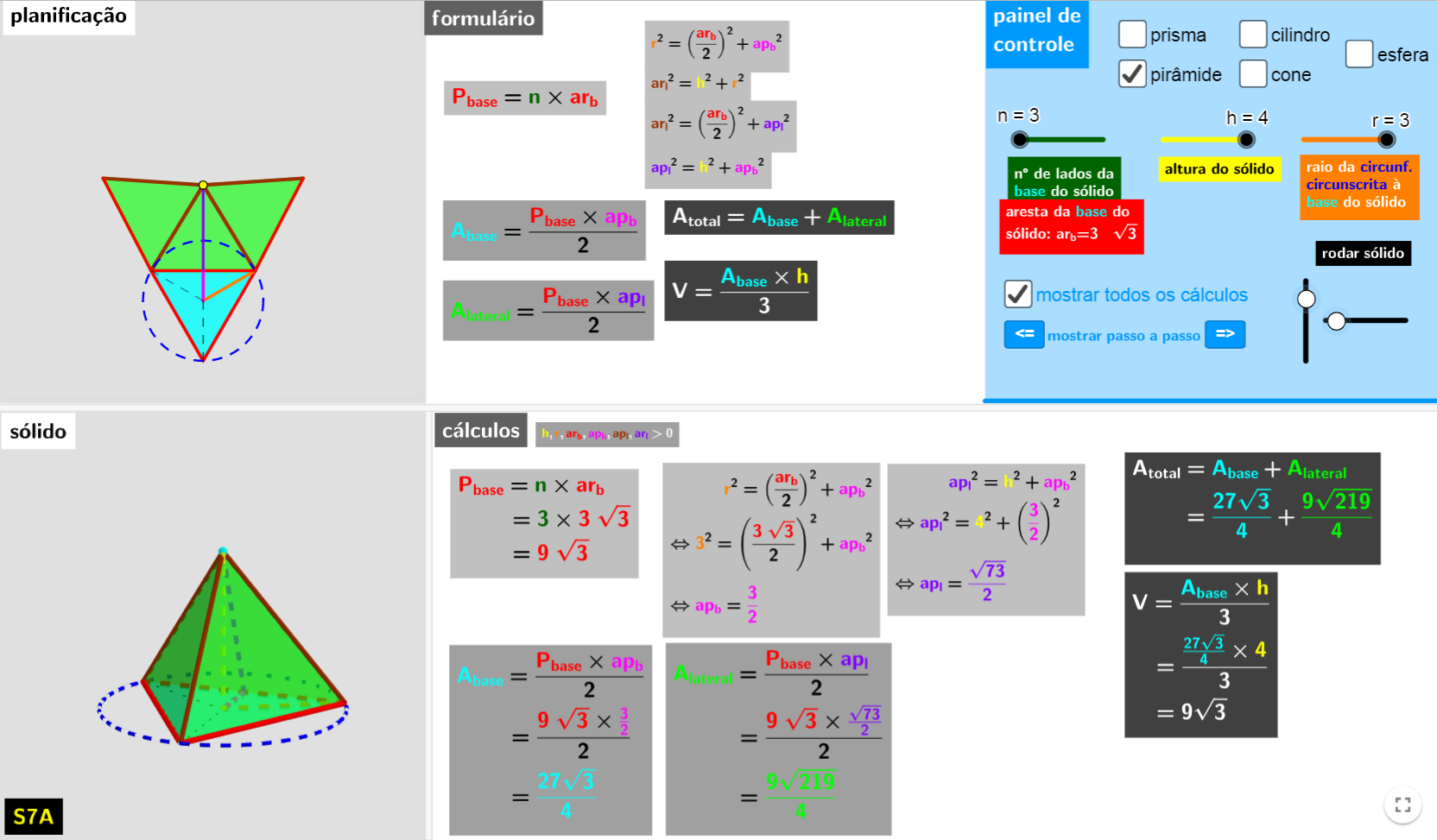
Permite conhecer a planificação de alguns sólidos retos/regulares em função das suas medidas, bem como os cálculos necessários à obtenção das medidas dos seus volumes e áreas das superfícies.
As diferentes cores sugerem a utilização das respetivas medidas no formulário.
O simulador tem 5 regiões:
☐ sólido – apresenta o sólido; premir o botão direito do rato e mexer rato faz rodar a vista 3D;
☐ planificação – apresenta a planificação do sólido; não permite interação;
☐ fórmulário – apresenta o formulário necessário aos cálculos intermédios e finais para obtenção das medidas do volume e áreas da superfície (da base, lateral e total) do sólido; não permite interação;
☐ cálculos – apresenta os cálculos intermédios e finais para obtenção das medidas do volume e áreas da superfície (da base, lateral e total) do sólido; não permite interação;
☐ painel de controle (região azul) – onde a interação é feita:
• Selecionar o sólido pretendido
• Deslizar os sliders para alterar as suas medidas/características;
• Deslizar os sliders pretos permite fazer rodar o sólido;
• Marcar “mostrar todos os cálculos” permite mostrar todo o formulário e cálculos
• Desmarcar “mostrar todos os cálculos” permite utilizar as setas azuis para fazer avançar ou recuar a apresentação do formulário e cálculos.
Clicar na seta azul para avançar (=>) altera:
- A região formulário (apresentando passo a passo a obtenção das fórmulas finais de Área total da superfície e Volume do Sólido), dando algumas indicações em texto sobre a obtenção das fórmulas;
- A região cálculos (apresentando passo a passo os valores dos cálculos intermédios e finais para a obtenção das medidas da Área total da superfície e Volume do Sólido);
- A região sólido fazendo sobressair a preto os triângulos retângulos que justificam a utilização do Teorema de Pitágoras para relacionar medidas de altura, raio, apótemas, arestas e geratrizes.