Relembra:
Conjunto dos números naturais: 
= {1,2,3,...}
Conjunto dos números inteiros:
= {...-3, -2, -1, 0, 1, 2, 3,...}
Conjunto dos números racionais:
= ∪ {números fraccionários}
Conjunto dos números reais:
= ∪ {números irracionais}
Os números racionais são os números reais que se podem representar sob a forma de fracções "a sobre b" , com termos inteiros (b ≠ 0), ou seja, sob a forma de dízimas finitas ou infinitas periódicas.
Os números irracionais são os números reais que podem ser representados por dízimas infinitas não periódicas.
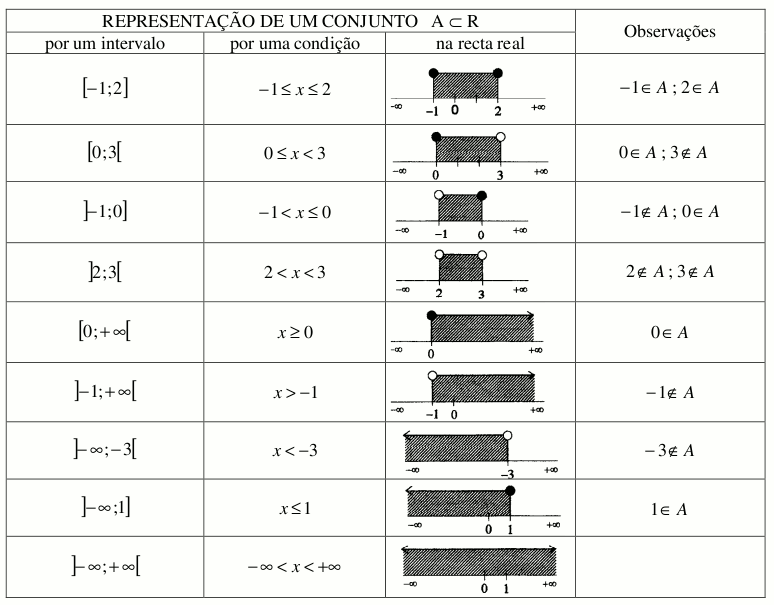
A reunião de intervalos representa-se por ∪ e contém todos os elementos desses intervalos.
A intersecção de intervalos representa-se por ∩ e contém apenas os elementos comuns aos intervalos.
Uma inequação do 1º grau a uma incógnita é uma condição com uma variável do 1º grau, que relaciona duas expressões através dos sinais de desigualdade > ou < ( ≥ ou ≤ ).
Uma solução de uma inequação é um valor do domínio que a satisfaz, ou seja, concretizado na incógnita transforma-a numa desigualdade verdadeira.
O conjunto – solução de uma inequação é o conjunto de todas as soluções dessa inequação. Pode representar-se graficamente, através de condições ou por um intervalo de números reais.
Para resolver uma inequação seguem-se os mesmos princípios das equações, com a seguinte excepção: se a < 0,
ax < b muda-se o sinal da desigualdade e faz-se:
⇔ x > b
a
Se ligarmos duas inequações pela palavra e (simbolicamente ∧ ) obteremos a conjunção dessas inequações. O conjunto - solução é a intersecção dos conjuntos- solução de cada uma das inequações.
Se ligarmos duas inequações pela palavra ou (simbolicamente ∨ ) obteremos a disjunção dessas inequações. O conjunto - solução é a reunião dos conjuntos-solução de cada uma das inequações.
= {1,2,3,...}Conjunto dos números inteiros:
= {...-3, -2, -1, 0, 1, 2, 3,...}Conjunto dos números racionais:
= ∪ {números fraccionários}Conjunto dos números reais:
= ∪ {números irracionais}Os números racionais são os números reais que se podem representar sob a forma de fracções "a sobre b" , com termos inteiros (b ≠ 0), ou seja, sob a forma de dízimas finitas ou infinitas periódicas.
Os números irracionais são os números reais que podem ser representados por dízimas infinitas não periódicas.
A reunião de intervalos representa-se por ∪ e contém todos os elementos desses intervalos.
A intersecção de intervalos representa-se por ∩ e contém apenas os elementos comuns aos intervalos.
Uma inequação do 1º grau a uma incógnita é uma condição com uma variável do 1º grau, que relaciona duas expressões através dos sinais de desigualdade > ou < ( ≥ ou ≤ ).
Uma solução de uma inequação é um valor do domínio que a satisfaz, ou seja, concretizado na incógnita transforma-a numa desigualdade verdadeira.
O conjunto – solução de uma inequação é o conjunto de todas as soluções dessa inequação. Pode representar-se graficamente, através de condições ou por um intervalo de números reais.
Para resolver uma inequação seguem-se os mesmos princípios das equações, com a seguinte excepção: se a < 0,
ax < b muda-se o sinal da desigualdade e faz-se:
⇔ x > b
a
Se ligarmos duas inequações pela palavra e (simbolicamente ∧ ) obteremos a conjunção dessas inequações. O conjunto - solução é a intersecção dos conjuntos- solução de cada uma das inequações.
Se ligarmos duas inequações pela palavra ou (simbolicamente ∨ ) obteremos a disjunção dessas inequações. O conjunto - solução é a reunião dos conjuntos-solução de cada uma das inequações.