Para desenhar o
ponto vermelho ou
a região a vermelho devemos:

1.º
Abrir compasso com a ponta seca po ponto Eva e raio x
(para medir x
usar régua ou escala gráfica fornecida)

1.º
Desenhar circunferência seguindo os passos acima
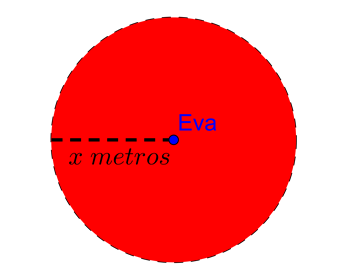
1.º Desenhar circunferência seguindo os passos anteriores
2.º Pintar interior da circunferência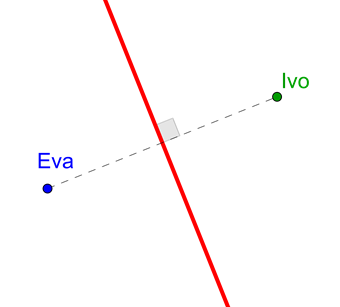
Seguir
o exemplo:
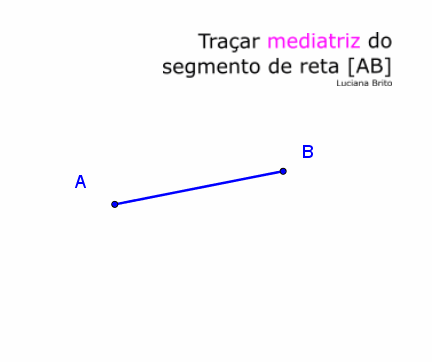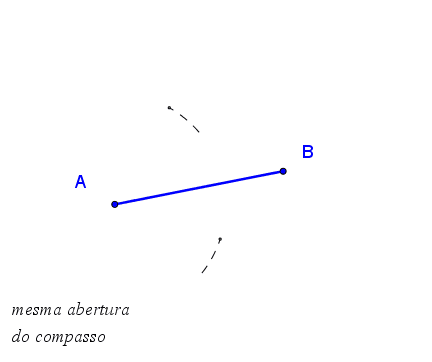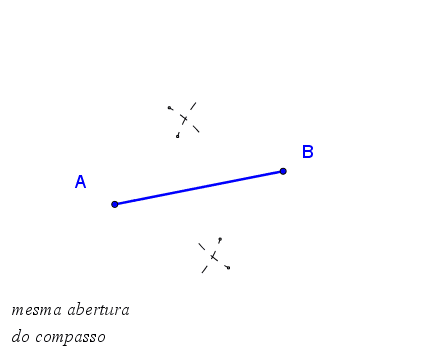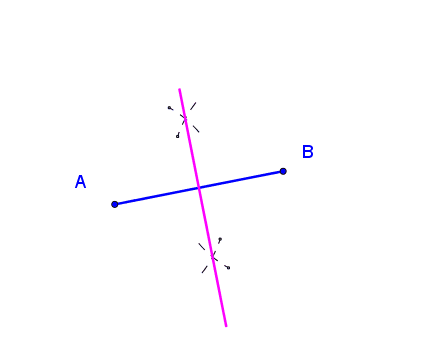
1.º
Abrir compasso com a ponta seca no ponto Eva e raio mais da metade da
distância entre a Eva e o Ivo
2.º Fazer pequenos arcos acima e abaixo do
segmento de extremos Eva e Ivo
3.º Repetir 1.º e 2.º mas com a ponta seca no Ivo e
marcar os pontos em que os pequenos arcos se intersetaram
4.º Pousar a régua sobre esses pontos e
desenhar a reta
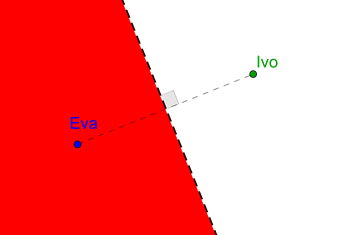
1.º
Desenhar mediatriz do segmento de reta de extremos na Eva e no Ivo
seguindo os passos acima
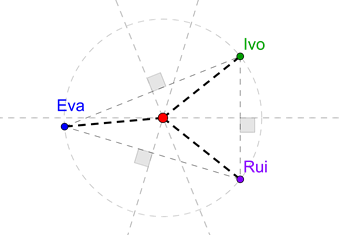
Seguir
exemplo:
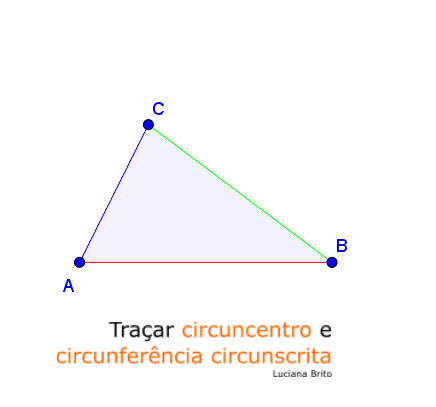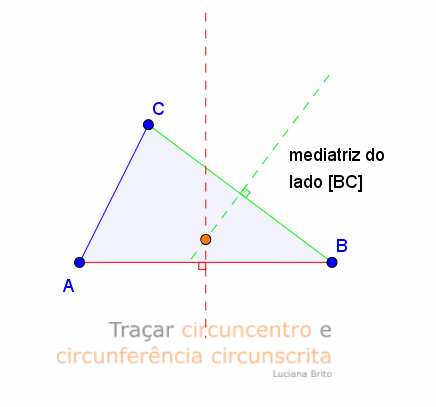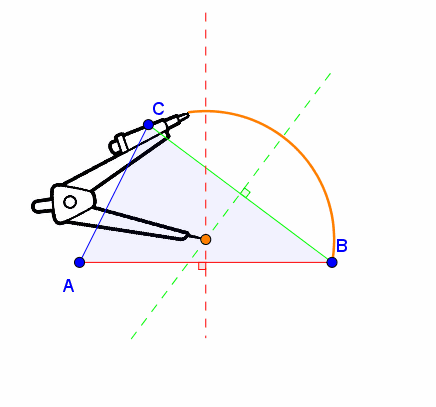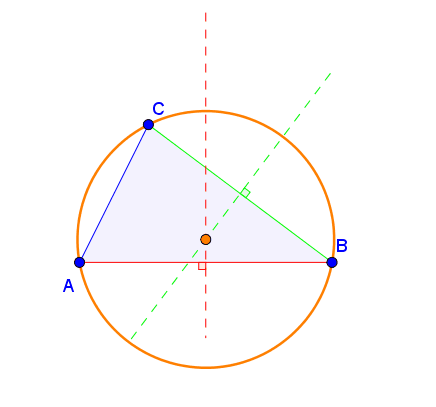
1.º
Desenhar mediatriz do segmento de reta de
extremos Eva e Ivo seguindo os passos anteriores
2.º Repetir 1.º para o segmento de reta de
extremos Eva e Rui
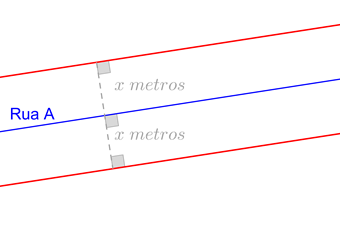
1.º
Utilizar esquadro para garantir que há perpendicularidade: colocar
cateto sobre a Rua A e desenhar perpendicular
2.º
Na perpendicular marcar ponto a x
cm de distância da Rua A
3.º
Repetir 1º e 2º noutro local da Rua A
4.º
Pousar a régua sobre esses pontos e desenhar a
reta
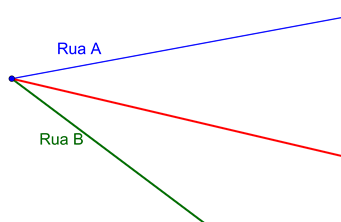
Seguir
exemplo:
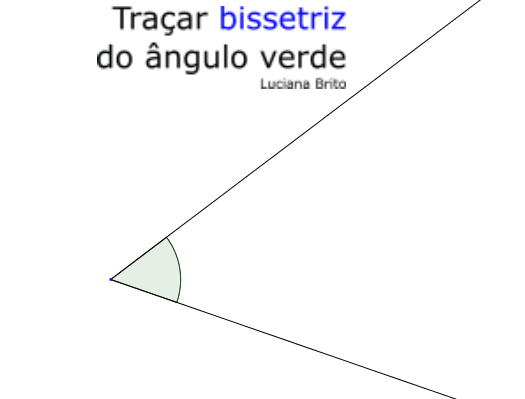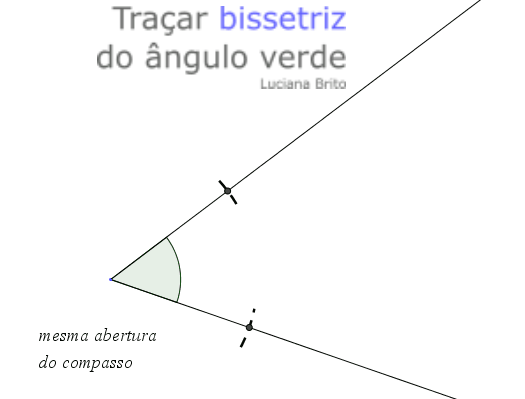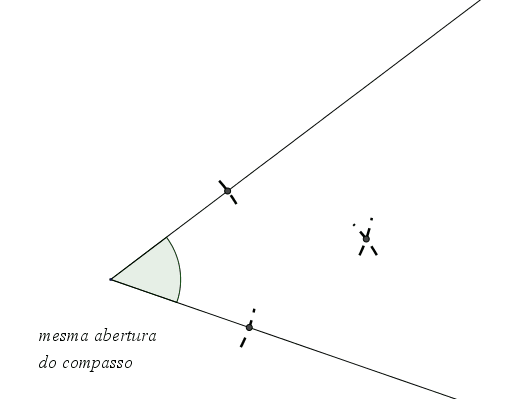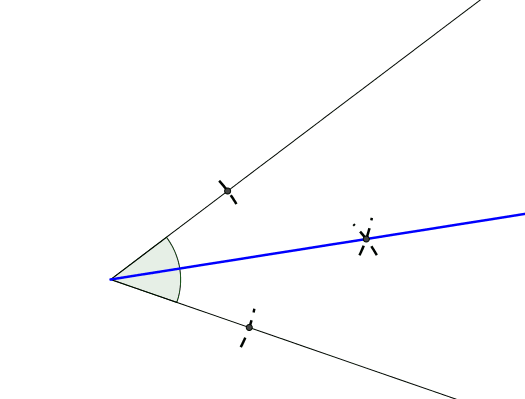
1.º
Abrir compasso com a ponta seca no vértice
do ângulo e intersetar as Ruas A e B com pequenos arcos
2.º Colocar a ponta seca do compasso sobre o ponto de interseção do
pequeno arco na Rua A e fazer outro pequeno arco
sensivelmente "a meio" do ângulo
3.º Repetir 2.º mas com a ponta seca sobre o ponto de interseção do
pequeno arco na Rua B e marcar o ponto de
interseção desse dois arcos
e
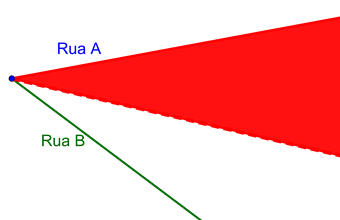
1.º
Desenhar bissetriz do ângulo formados pelas Ruas A e B seguindo os passos acima
2.º
Pintar região acima da bissetriz, que
é a que contém a Rua
A
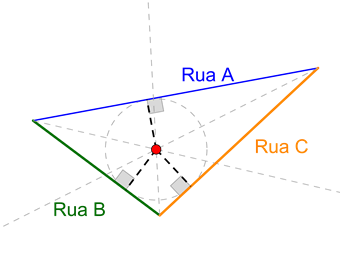
Seguir
exemplo:
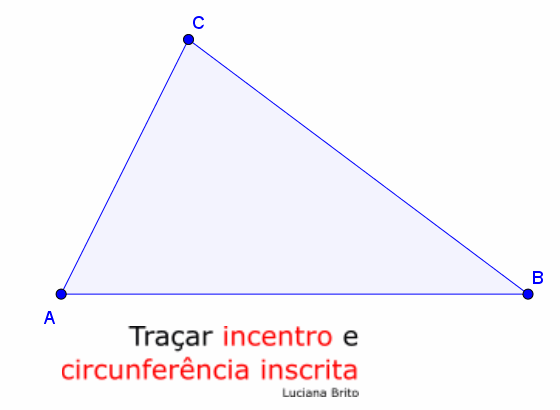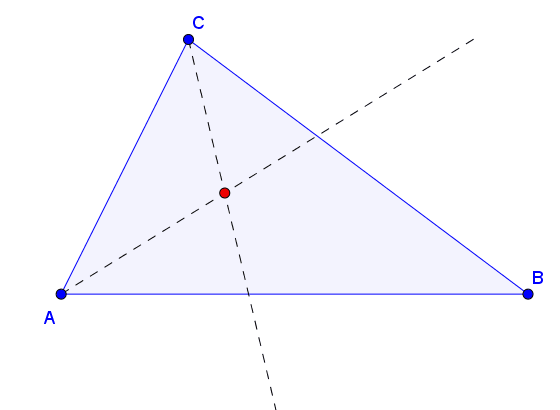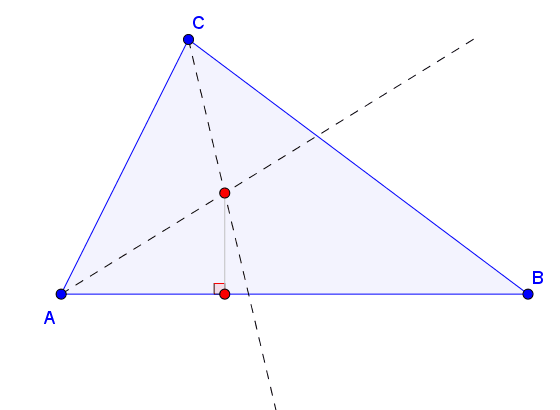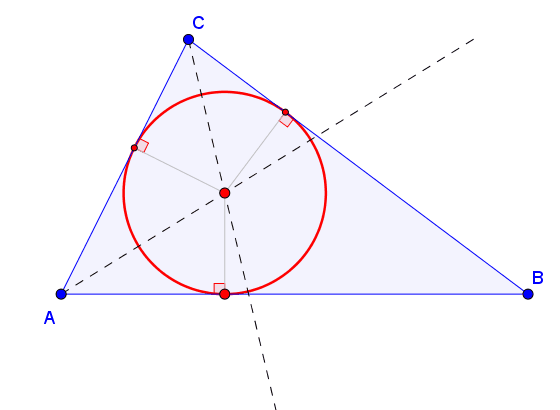
1.º
Desenhar bissetriz do ângulo formados
pelas Ruas A e B seguindo
os passos anteriores
2.º Repetir 1.º para as Ruas B e C